Evolution
Contents
Evolution¶
Day 1; Responses template for use on computer if desired
Day 2; Responses template for use on computer if desired
Complete this section prior to class and bring your responses with you (but you do not need to hand them in)
⏳ 10-20 min
Use the Intro section of the following simulation to examine the interaction between selection pressures and the phenotypic distribution of a population. Focus on the phenotypes, phenotype frequencies, and selection pressures. Do not focus on the issues of dominant/recessive alleles and allele frequency.
Once you start the simulation, add a mate and introduce a dominant mutation. Let the populaton grow for 2-3 generations before manipulationg any of the other factors in the simulation. Then experiment with different available manipulations and take notes on the results you observe across manipulations that you try.
HQ1: In this simulation, which bunny phenotype could vary?
HQ2: In this simulation, what were the three potential selective pressures that you could manipulate?
HQ3: In this simulation, what were the selective pressures that effected relative phenotype distributions in the bunny species?
General evolutionary concepts¶
A soft warm-up for class.
⏳ 5 min
To the best of your group’s ability…
Q1: Define ‘adaptation’
Q2: What is the main difference between ‘evolution’ and ‘natural selection’?
Q3: Does natural selection cause trait variation?
⏸️ PAUSE here for class-wide discussion
Selective Pressure¶
Why?
A fundamental assumption in the contemporary study of animal behaivor, is that behavior is both heritable1 and an adaptation (to changing needs and to a changing environment) that maximizes evolutionary fitness2 (ie. it evolves by natural selection).
Case Study on adaptation: exploitation of behavioral patterns¶
Behavioral patterns that are stereotyped (ie. FAPs) are, by definition, predictable. As you know from experiments that test for sign stimuli of FAPs, if a sign stimulus is encountered, then the FAP will be released, regardless of the source of that sign stimulus3. This sign stimulus : FAP pair can be thought of as a code. Code breaking describes the “inappropriate” release of an FAP by another animal.
In solitary ground nesting bee species (that includes the bee families: Andrenidae, Apidae, Colletidae, and Halictidae), females dig nests in which they deposit and provision their fertilized eggs with pollen after mating4.

Fig. 14 Left: a female solitary bee collecting pollen. Right: a female solitary bee provisioning its egg in a nest.¶
Males desperately seek females to mate with. They patrol nesting areas in large numbers and form ‘mating balls’ in which multiple males grapple with each other and attempt to pair up with the female56. The mating sequence of males comprises several FAPs that are organized according to stereotyped transition probabilities6.
But, males also “mate” with aggregates of larval blister beetles. During attempted copulation, the larvae hitch a ride on the male. When the male bee later mates with a female bee, the larvae can then transfer to the female and hitch a ride back to the female’s nest. The larvae are parasitic and feed off of the provisions in the nest that were intended for the bee larvae.

Fig. 15 Top Left: A female blister beetle depositing eggs on a plant stalk. Top Right: Days after hatching, the larval blister beetles aggregate with their brown heads pointing outward. Bottom. A male mates with a female bee after a mating attempt with the aggregation of larval blister beetles.¶
⏳ 10 min
Q4: Based on the information given, what do you think could be the sign stimulus that releases mating FAPs in the male bee? Name at least two potential alternatives.
Q5: Under the assumption that behaviors are “adaptations”, what is the paradox in this example?
Q6: Brainstorm potential “selective pressures” affecting the existence of this “sign stimulus - FAP pair” in male bees
⏸️ PAUSE here for class-wide discussion
Evolutionary Models¶
Why?
Ultimately, to understand a behavioral phenotype from an evolutionary perspective means to be able to predict phenotypes of extant species (ie have an accurate model).
Models are abstractions that strive to have predictive power (with varying degrees of precision). Models represent a best informed guess as to the identity and function of important variables and how these variables interact. They are commonly formulated mathematically.
Two of the most common types of evolutionary models are Optimality Theory and Game Theory
Optimality Theory¶
Remember observing and quantifying vigilance behavior in meerkats? From an evolutionary perspective, let’s learn how to understand vigilance behavior using an optimality theory modeling approach.
Consider the two alternative behavioral phenotypes:
vigilant: animals are sometimes vigilant
not vigilant: animals are never vigilant.
Let’s start by examining two factors that likely exert selective pressure on this behavioral variation:
time available to forage (searching for and eating food)
likelihood of being injured/killed by a predator
⏳ 5
Q7: In terms of time foraging and/or likelihood of being injured/killed by a predator, what is the ‘benefit’ of a vigilant phenotype compared to not vigilant?
Q8: In terms of time foraging and/or likelihood of being injured/killed by a predator, what is the ‘cost’ of a vigilant phenotype compared to not vigilant?
Q9: In terms of time foraging and/or likelihood of being injured/killed by a predator, what is the ‘benefit’ of a not vigilant phenotype compared to vigilant?
Q10: In terms of time foraging and/or likelihood of being injured/killed by a predator, what is the ‘cost’ of a not vigilant phenotype compared to vigilant?
⏸️ PAUSE here for class-wide discussion
We often come across evolutionary explanations in terms of costs and benefits. As you see from this example, these terms are relative. Therefore, it is more generalizable to talk in terms of factors rather than costs or benefits per se.
⏳ 10
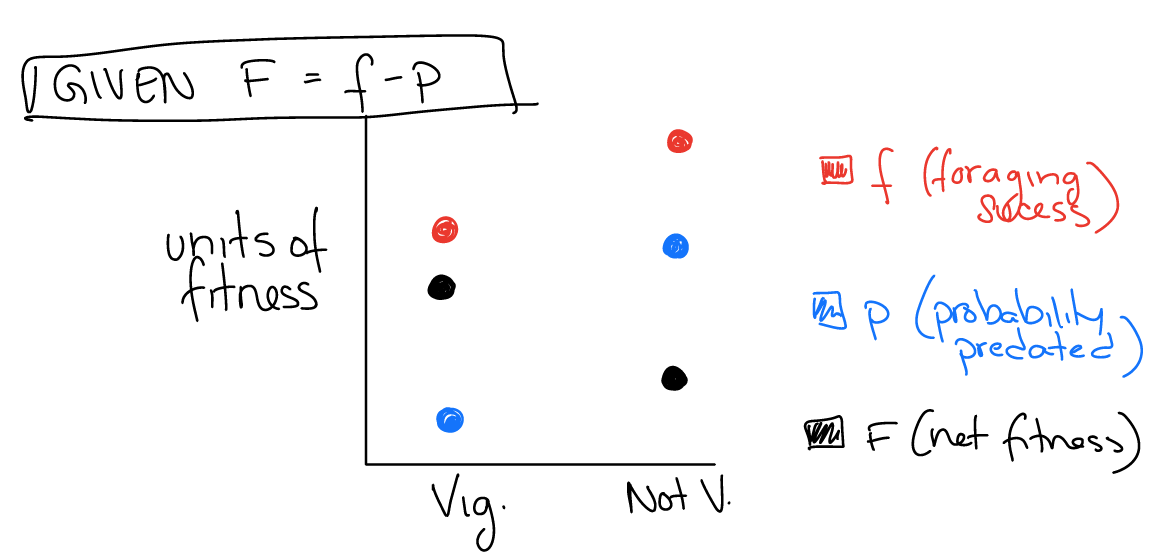
Let’s formalize an optimality theory model for \(F\), the net fitness of a phenotype, in terms of the two factors you just examined.
where \(f\) = foraging success (amount and quality of food eaten) and \(p\) = likelihood of being injured/killed by a predator.
If there are multiple possible phenotypes (in this case vigilant or not vigilant), then, by optimality theory, the phenotype that confers greater total fitness to the animal will be favored by natural selection. Therefore, the solution to an optimality model is to figure out which phenotype has a highest net fitness (\(F\)).
Q11: Would the vigilant phenotype or the not vigilant phenotype have a higher value of \(f\)?
Q12: Would the vigilant phenotype or the not vigilant phenotype have a higher value of \(p\)?
Q13: Given this information, can you determine which phenotype has a higher net fitness? Choose some logical estimates for values of the model variables (\(f\) and \(p\)) to make your prediction.
Q14: What kinds of issues are you encountering in using the model to predict which phenotype is more fit?
⏸️ PAUSE here for class-wide discussion
Consider how environments can differ. Do all environments have the same amount or quality of food? What about predators? As you experienced in the Natural Selection Simulation, changing environments can change the relative fitness of a set of phenotypes… but how?
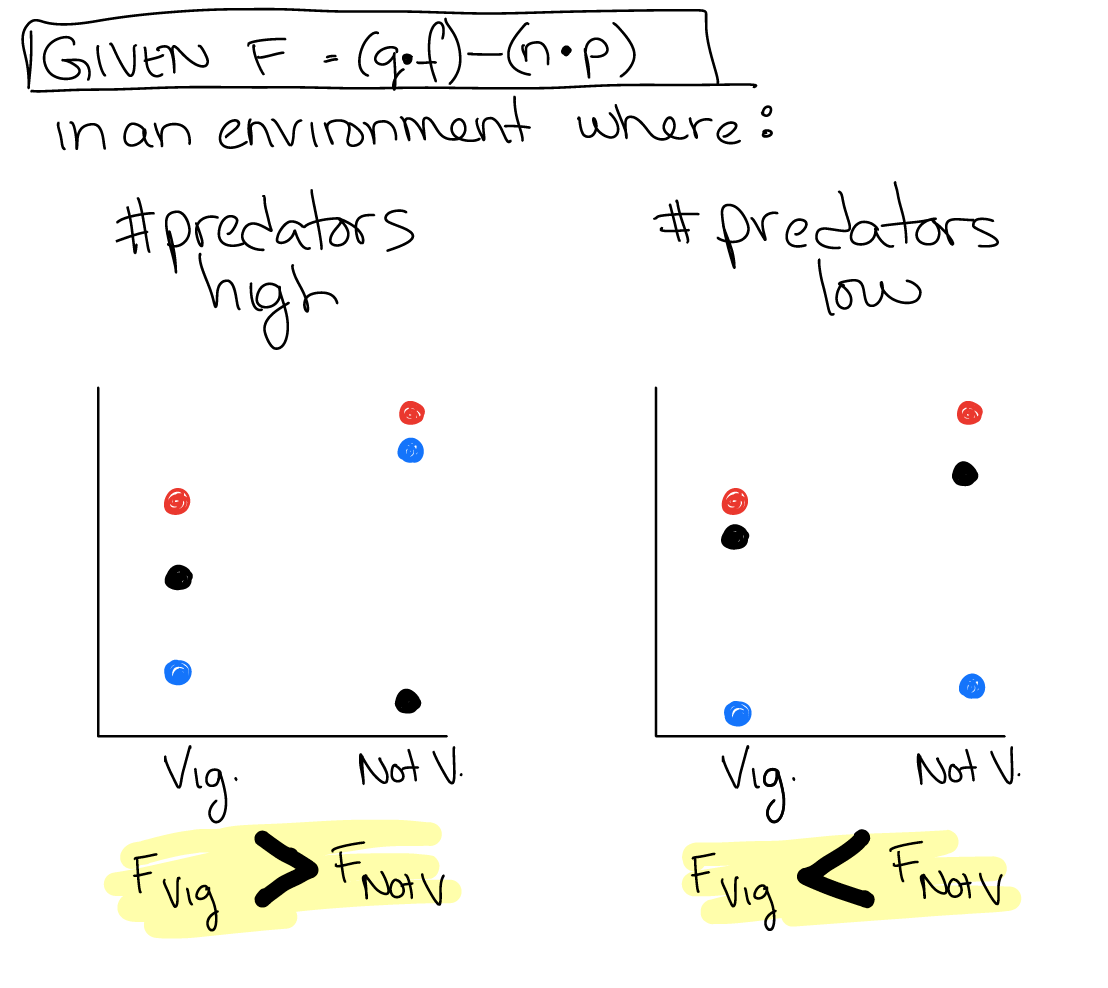
Let’s account for the effect of environment by adding two new variables to the model:
\(q\) = the quality or amount of food available
\(n\) = the number of predators
Consider this revised formulation of the model
⏳ 10
Q15: Based on this revised model, in an environment with a lot of predators and low food quality, which phenotype would you predict to be favored by natural selection?
Q16: Does this revision of the model change your ability to solve the model? If so, then in what ways? If not, then why not?
Q17: Given that the models you just explored were examples of ‘Optimality Theory Models,’ how would you define ‘optimality theory’?
Q18: What would you do next if your model did not correctly predict vigilance behavior of a population that you were studying?
⏹️ STOP here for today
Game theory¶
There are many cases in which the fitness associated with a particular behavior depends on what other conspecifics7 are doing. Thus, what is evolutionarily favored will depend on the distribution of phenotypic variation in the population (and therefore on the likelihood of certain phenotypes interacting, each with different fitness consequences). Game theory is like optimality theory in many ways, but it takes into account selective pressure from conspecific phenotypes and the proportion in which other phenotypes exist.
Let’s work through the logic of a game theory modeling approach by role-playing a common example from conflict resolution behavior. In the basic form of this model, there are two possible behavioral phenotypes: fighter and pacifist.
Setting up the conflict resolution game theory model
There are two possible behavioral strategies (phenotypes)
Fighters always fight when challenged until the resource is won. In the simplest case, each fighter has a 50% chance of winning the resource.
Pacifists share the resource, and back down immediately when challenged with a fight (they don’t engage in any fighting, which means they give up the resource completely when challenged, but also don’t get injured from fighting).
There are two factors that can contribute to an animal’s fitness
the energy gained by obtaining the limited resource
the damage done by losing a fight over a resource (the consequence of losing a fight)
What happens when each set of behavioral strategies interact?
⏳ 15
Play it out
Choose two people from the group to be the ‘players’. Players act out the game from the perspective of the behavioral phenotypes (strategies). There are two different conditions to act out, as described below.
Choose one person from the group to be the moderator. The moderator starts each round.
Choose one person from the group to keep track of each player’s fitness in the game.
Condition 1: A population of Pacifists Each player represents the pacifist phenotype.
The moderator places one blue pen on the table. This pen is the ‘resource’ and it is worth +2 units of fitness.
When the moderator says go, both players interact over the resource. Decide how the resource will be allocated according to the ‘pacifist’ behavioral strategy described in the model setup.
After the resource has been allocated, tally the net change in each player’s fitness as a consequence of the encounter.
The moderator places the blue pen back on the table and the interaction repeats (ie trial #2) when the moderator says go.
Repeat the interaction for 10 trials total (tallying each player’s change in net fitness after every encounter)
Condition 2: A population of Fighters Each player represents the fighter phenotype.
The moderator places one blue pen on the table. This pen is the ‘resource’ and it is worth +2 units of fitness.
The moderator places one red pen on the table. This pen is the consequence of losing a fight and it is worth -1 unit of fitness.
When the moderator says go, both players interact over the resource. Decide how the resource and consequence will be allocated according to the ‘fighter’ behavior described in the model setup.
After the resource and consequence have been allocated, tally the net change in each player’s fitness as a consequence of the encounter.
Repeat the interaction for 10 trials total (tallying each player’s change in net fitness after every encounter)
Q1: Which behavioral phenotype would result in a “more fit” population?
⏸️ PAUSE here for class-wide discussion
⏳ 10
Play it out
Condition 3: Pacifist and Fighters mix One player represents the pacifist phenotype. The other player represents the fighter phenotype.
The moderator places one blue pen on the table representing a ‘resource’ worth +2 units of fitness.
The moderator places one red pen on the table representing the consequence of losing a fight and it is worth -1 unit of fitness.
When the moderator says go, both players interact over the resource. Decide how the resource and consequence will be allocated according to the pacifist behavior encountering a fighter behavior (and vice versa) as described in the model setup.
After the resource and consequence have been allocated, tally the net change in each player’s fitness as a consequence of the encounter.
Repeat the interaction for 10 trials total (tallying each player’s change in net fitness after every encounter)
Q2: Based on your results of all three simulations, make a table that documents the average net fitness that you tallied for each behavioral strategy (pacifist and fighter; rows) in each behavioral context (pacifist and fighter; columns).
⏸️ PAUSE here for class-wide discussion
The game theory model that you have been playing out can be formulated using the following equations, where \(v\) is the value of the resource and \(c\) is the consequence of losing a fight.
In a population of fighters |
In a population of pacifists |
|
|---|---|---|
Average net fitness for a fighter |
\({(v-c)}/2\) |
\(v\) |
Average net fitness for a pacifist |
0 |
\(v/2\) |
After a fighter encounters another fighter, its fitness changes by \( v \) if it wins but \(-c \) if it loses. Since it wins 1/2 the time, the average change in fitness is \(v/2 - c/2\).
After a pacifist encounters another pacifist, its fitness changes by \(v/2\) because they share the resource.
Fighters always gain the resource against pacifists and do so without a fight, which means pacifists end up with nothing against fighters.
In the conditions that you acted out, \(v=2\) and \(c=1\).
We can use the model equations to determine what phenotype (or mix of phenotypes) would be evolutionarily stable under a particular set of conditions.
- evolutionary stability/equilibrium¶
An evolutionarily stable phenotype is one that cannot be invaded by another phenotype – it persists in the face of natural selection. At evolutionary equilibrium, populations can either exhibit one stable phenotype or a stable mixture of phenotypes.
⏳ 10
Q3: According to the proposed model, the fitness of the fighter phenotype (DOES / DOES NOT) depend on the behavioral phenotype of conspecifics. When conspecifics are all fighters, the average fitness of fighting is ________. When conspecifics are all pacifists, the average fitness of fighting is ________.
Q4: Under the conditions \(v=2\) and \(c=1\) (that you acted out), use the model equations to determine which strategy has a greater net fitness in a population of all pacifists.
If pacifists have a greater net fitness than fighers in a population of pacifists, then the fighting phenotype cannot invade – and pacifist would be the evolutionarily stable strategy predicted by the model. However, if fighers have a greater net fitness than pacifists, then we would predict that a population of pacifists would not be stable at evolutionary equilibrium. And vice versa…
Q5: Under the conditions \(v=2\) and \(c=1\) (that you acted out), use the model equations to determine which strategy has a greater net fitness in a population of all fighters.
⏸️ PAUSE here for class-wide discussion
⏳ 5
Consider a new set of conditions. For example, what about an environment in which there are more predators. In this environment, the cost of losing a fight may be greater because if you are injured, you have a high probability of being eaten by a predator. Consider now that \(v=2\) and \(c=3\).
Q6: In this different environment, where v=2 and c=3, is there one strategy that would be evolutionarily stable? If so, which one?
⏸️ PAUSE here for class-wide discussion
Game theory models like the pacifist : fighter model you have been considering, are often represented in the following tabular format. It is worth getting familiar with this way of representing game theory models, because using the table aids in model analyis (makes the process of solving the model more algorithmic).
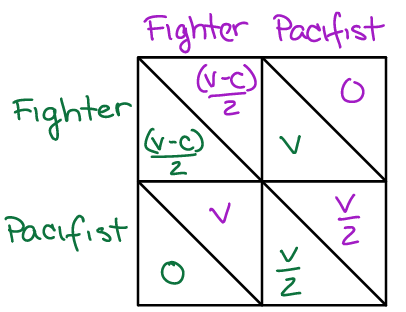
Fig. 16 A tabular representation of the game theory model of conflict resolution behavior that includes pacifist and fighter phenotypes. Each box of the table is split by a diagonal line. The fitness of each phenotype in each player role (green or purple) is written to the left or right (respectively) of each diagonal line. Note that this model is symmetric (there is only one type of individual/role that could exhibit each behavior) – this is not always the case.¶
General solutions to the model¶
One task of both optimality theory and game theory models is to determine under what conditions (range of values for the factors) is each behavior(s) stable. However, the algorithm for solving the game theory models in this way can get a bit more complex than Optimality Theory.
For example, fighting is “stable” when the strategy cannot be invaded by the pacifist strategy. This is only true when pacifists have a lower average fitness than fighters when in a population of fighters (ie. a mutant pacifist). Mathematically, this statement would be written: Fighting is a stable strategy when \({(v-c)}/2 > 0\). Simplifying the equation gives the condition: \(v > c\).
⏳ 5 min
Q7: Are there conditions under which the pacifist phenotype would be evolutionary stable? To solve this problem, use the model equations to set up the inequality that asserts “pacifists have a greater net fitness than fighters” in a population of all pacifists. Then simplify the inequality. The result is the conditions under which pacifist would be stable.
⏸️ PAUSE here for class-wide discussion
⏳ 5 min
Q8: Are there conditions under which a species would be comprised of BOTH pacifists and fighters simultaneously at evolutionary equilibrium? What inequalities would you need to set up to solve this?
⏸️ PAUSE here for class-wide discussion
Understanding MIXED behavioral phenotypes¶
It IS possible that there are conditions under which neither behavioral phenotypes alone are evolutionarily stable, but a population consisting of both co-existing phenotypes is. For example, we know of behavioral phenotypes that have higher fitness than the alternative only when that alternative exists.
Here are a few as examples:
sitter versus rover foraging behavior (fruit flies)
singing versus silent mate attraction behavior (crickets)
fighter versus pacifist resource conflict resolution (when the cost of losing a fight is high)
sneaky versus dominant versus monogamous mating behavior (side-blotched lizards… see video and game theory model below)
The game theory model below summarizes the relative fitness of each mating behavior in the context of all others. These mating phenotypes have also been observed simultaneously in several other species of anmimals. \(F\) is the baseline fitness.
Dominant |
Sneaky |
Monogamous |
|
|---|---|---|---|
Dominant |
F |
F - 1 |
F + 1 |
Sneaky |
F + 1 |
F |
F - 1 |
Monogamous |
F - 1 |
F + 1 |
F |
Simulating this game theory model gives the following result:
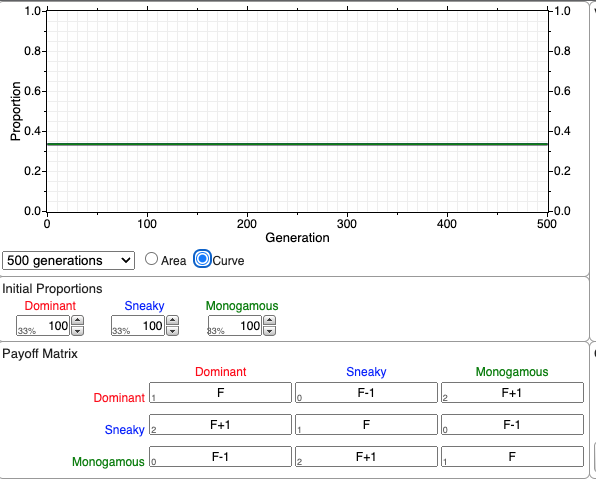
All three behavioral phenotype exists simultaneously at evolutionary equilibrium (after many generations of time). No one individual behaivor is ever evolutionarily stable (ie. we would never predict a population of only Dominant mating behavior). The three phenotype variants exist with a frequency of 33.333% (1/3).
Let’s think about the following together:
If the population was initialized with fewer dominant phenotypes (ie. there are very few dominant individuals in the population) and equal sneaky and monogamous, which phenotype would we expect to increase in frequency: sneaky or monogamous?
Once that phenotype dominated, which phenotype would then have the highest net fitness?
We can simulate #1 and #2 to test our predictions. This Demo Simulation (popup) is a good resource for gaining more intution for the interactions among phenotypes.
⏹️ STOP here for today
Additional Resources¶
This video is a simulation on the evolution of conflict resolution behaviors that provides a nice perspective on the logic of game theory models in understanding behavior. Think about, what is the paradox here?
Silent versus Satellite Crickets: To mate or be eaten: tree cricket behaviour in the presence of a predator and Silent night: adaptive disappearance of a sexual signal in a parasitized population of field crickets and A simulation model of the effects of frequency dependence, density dependence and parasitoid flies on the fitness of male field crickets
Modeling Behavior: Game and Optimality Theory from Holy Cross College
Game Theory and Evolutionarily Stable Strategies from Holy Cross College
Game Theory Tutorial: Conflict, Probability, Stable Strategies
Fitzpatrick, M., Feder, E., Rowe, L. et al. Maintaining a behaviour polymorphism by frequency-dependent selection on a single gene. Nature 447, 210–212 (2007). provides and example of negative frequency-dependent selection in which the underlying genes for the behavioral variation is known.
Common Descent Podcast, Episode 56: The Evolution of Evolutionary Theory
Game Theory Tutorial: Conflict, Probability, Stable Strategies
- 1
A key assumption is that behavioral phenotypes are heritable across generations (that there is a strong genetic component, though we won’t get into any actual genetics yet). If an individual has an advantageous trait, then it is more likely to reproduce. Since traits pass from parents to offspring (heritability), then offspring are likely to inherit advantageous traits. Over time, advantageous traits become more common in a population.
- 2
In other words, behavior can convey reproductive advantage. We won’t by more explicit about fitness from the perspective of alleles themselves until we have reviewed Genetics as a class. When we talk about fitness, we can think about how well an animal survives. When we talk about phenotypes as adaptations and their evolution, we ultimately do need to think about fitness in terms of the frequencies of gene alleles that give rise to those phenotypes. Allele frequency over generations depends little on the survivability of an individual animal, and more on how much that animal reproduces (and how well its offspring reproduce).
- 3
There are many examples of the effect of a sign stimulus being inhibited by a concurrent, but different, stimulus. The effects of sign stimuli can also be enhanced by additional stimuli.
- 4
- 5
Busy Bees: An Up-Close Look at One Bee Species’ Scramble to Mate
- 6(1,2)
- 7
Conspecifics are individuals of the same species. In understanding the evolution of behavior, we consider phenotypic variation within a species, not between species.