Exponential Decay
Contents
Exponential Decay¶
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where N is the quantity and \(\lambda\) (lambda) is a positive rate called the exponential decay constant.
\[ \frac {dN}{dt}=-\lambda N\]The solution to this equation is
\[ N(t)=N_{0}e^{-\lambda t}\]where \(N(t)\) is the quantity at time \(t\), \(N0 = N(0)\) is the initial quantity, that is, the quantity at time \(t\) = 0, and the constant \(\lambda\) is called the decay constant (ie. space constant, time constant).
A neuron (or any cell) is a membrane-enclosed sphere/cylinder. A voltage applied across the membrane at one location decays along the length of the membrane. The extent of this decay is determined by the space constant. A current applied across the membrane at one location will take some time to generate a change in membrane voltage at that location. The time course of the change in voltage is determined by the time constant. We can understand these phenomena with some math and electronics.
Space Constant¶
For a neuron, the space constant is a measure of how far the voltage travels1 along the membrane.
Mathematically, the space constant (\(\lambda\)) is well-predicted by the equation
\(\lambda = \sqrt{R_m/R_i}\)
where \(R_m\) is the resistance across the membrane and \(R_i\) is the resistance of the intracellular fluid (axoplasm).
If you have a length constant of 1 mm, that means at 1 mm away from the cell body in an axon, 37% of the voltage magnitude remains. At 2 mm away from the cell body in an axon, 14% of the magnitude remains, and at 3 mm away, 5% remains. This is representative of an “exponential decay” function.
Modifying a neuron’s space constant¶
Myelin¶
Myelin is a fatty covering around the membrane that reduces the leakyness of the membrane (increases \(R_m\))2.
What has been generally borne out with computer simulations is that a myelinated neuron twice as thick as another myelinated neuron will have a conduction velocity twice as fast3.
Axon Diameter¶
The larger the radius of a neural compartment (ie. an axon), the smaller both \(R_i\) and \(R_m\) will be. Note that both \(R_i\) and \(R_m\) vary with the radius of the neuron’s membrane, but with different functions. \(R_m\) depends on the circumference by
where \(r_m\) is a constant that can be measured from the neuron regardless of its size.
While \(R_i\) depends on the area by
where \(r_i\) is a constant that can be measured from the neuron regardless of its size.
By combining these equations and simplifying by eliminating constants, we find that the length constant scales with the square root of the radius (\(\lambda \approx \sqrt{radius}\))
Time Constant¶
For a neuron, the time constant is a measure of how long (time) it takes for the memrbane to charge to a stable voltage in response to an applied current.
Mathematically, the time constant (\(\lambda\)) is well-predicted by the equation
\(\lambda = R_m * C_m\)
where \(R_m\) is the resistance across the membrane and \(C_m\) is the capacitance of the membrane. Capacitance effectively buffers otherwise sudden changes in voltage.
Neurophysiology of space and time¶
“Cable Theory”, was originally developed in the 1800’s when engineers were trying to understand signal transmission across long distance telegraph lines. Neuroscientists then applied this theory to neurons in the early 20th century.
Imagine a neuron with an infinitely high length constant. A voltage change anywhere in the neuron would instantly change the voltage everywhere else in the neuron. No such neuron exists.
Voltage propagation along a neuron membrane has a finite travel distance. Active (voltage-sensitive) ion conductances fight this decay by regenerating a trans-membrane voltage wherever they are activated (ie. an action potential). However, action potential propogation has a finite speed. Each time an ion channel needs to open to recharge the action potential, this delays the propagation of the action potential by approximately 1 ms. And the time constant of the membrane effects how quickly any patch of membrane will charge. Additionally, the smaller your length constant is, the more you have to regenerate the action potential by having ion channels open along the length of the axon.
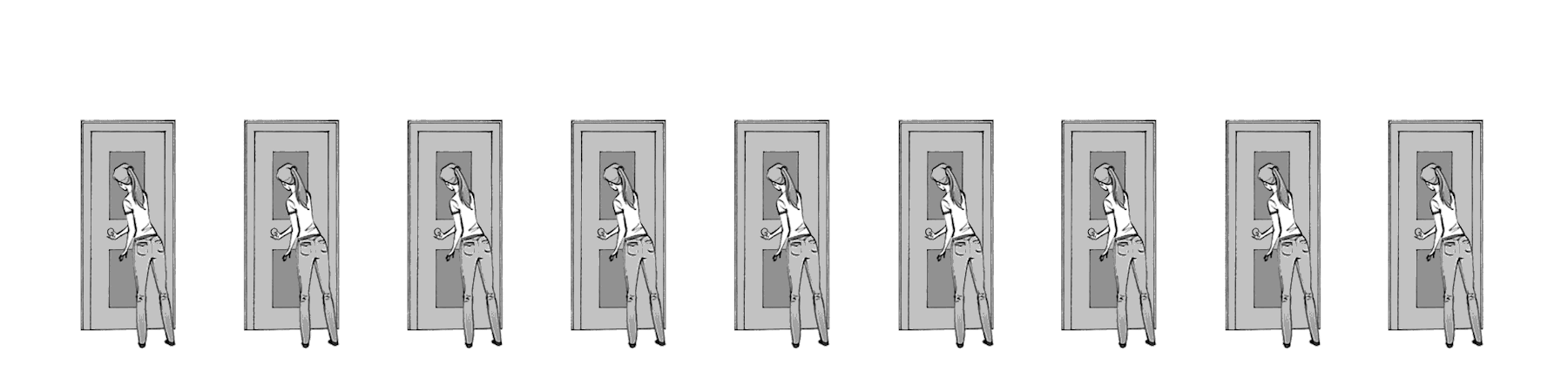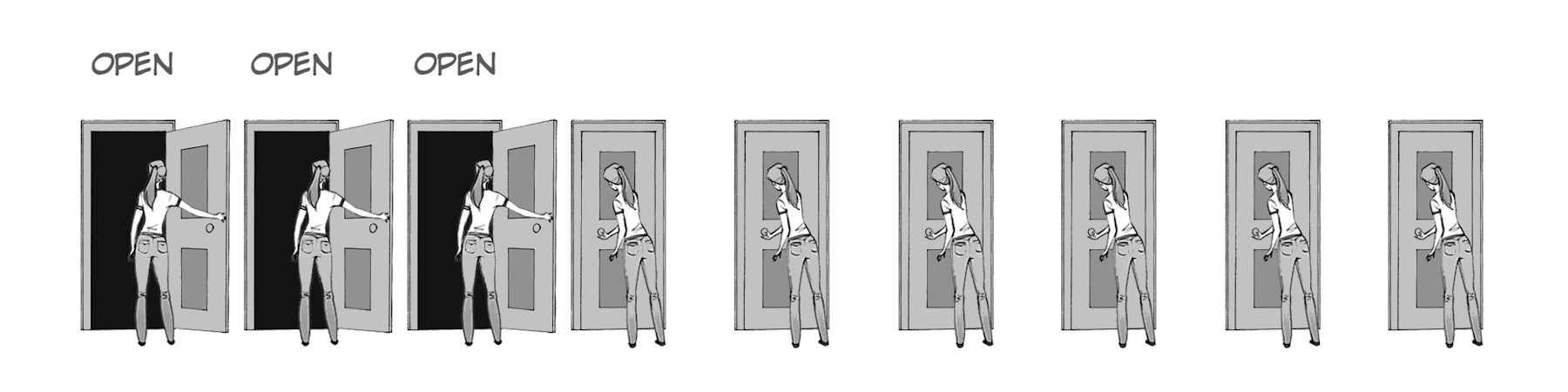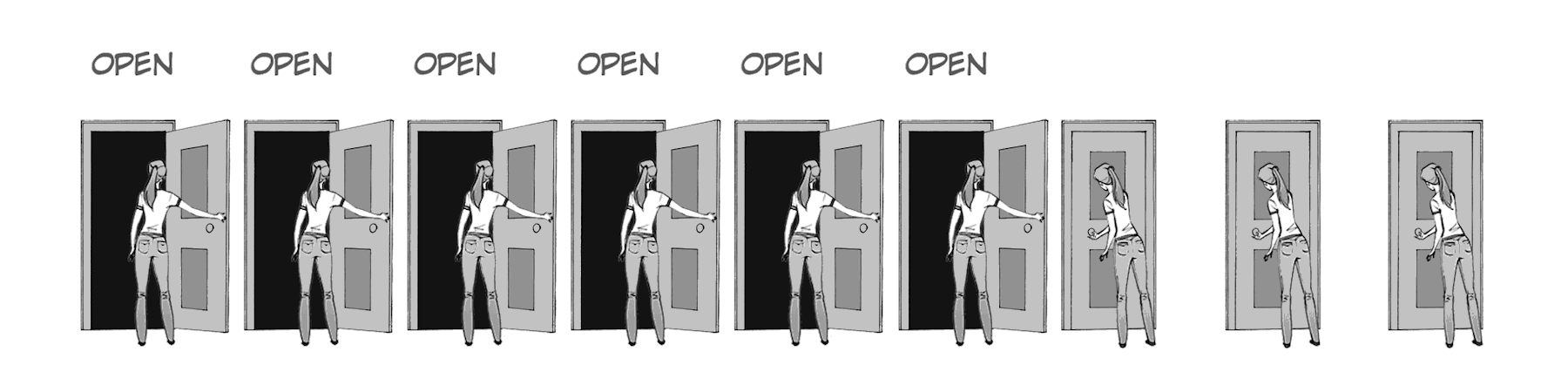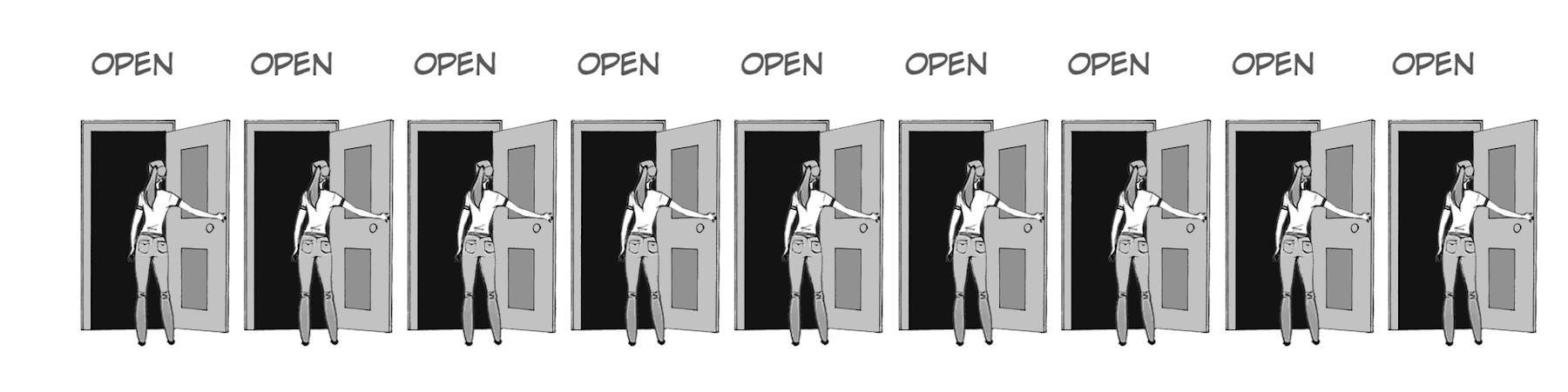
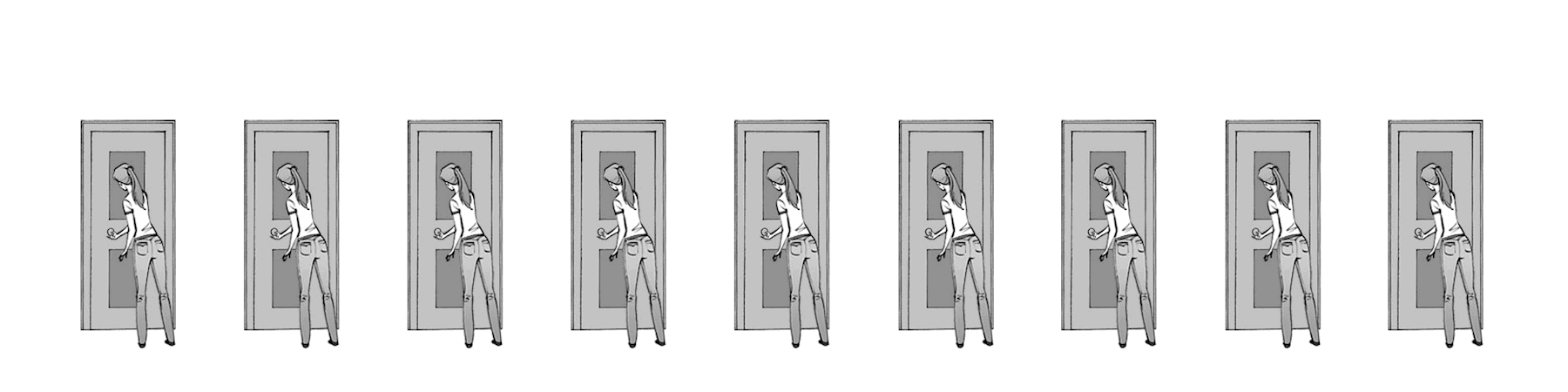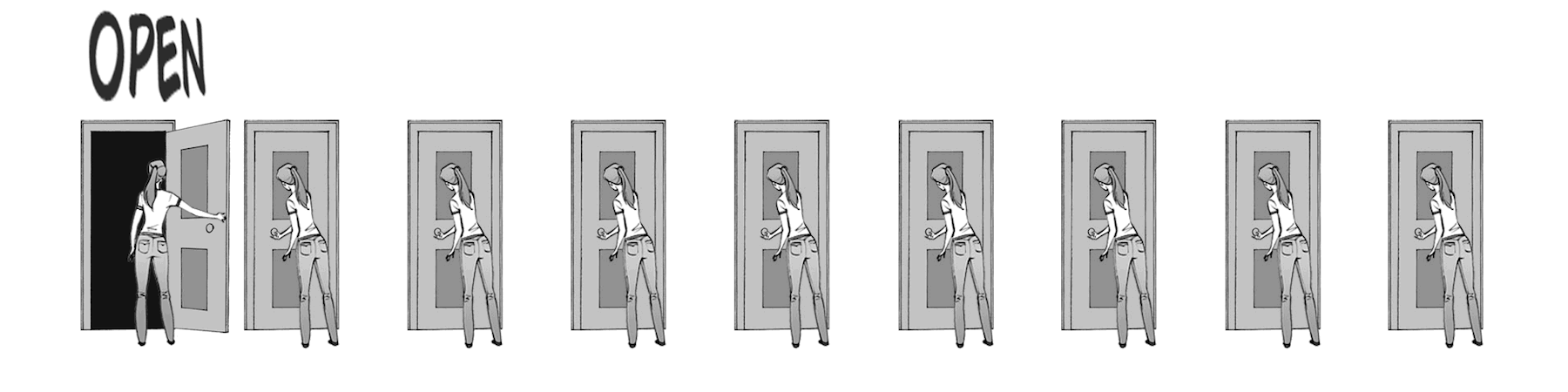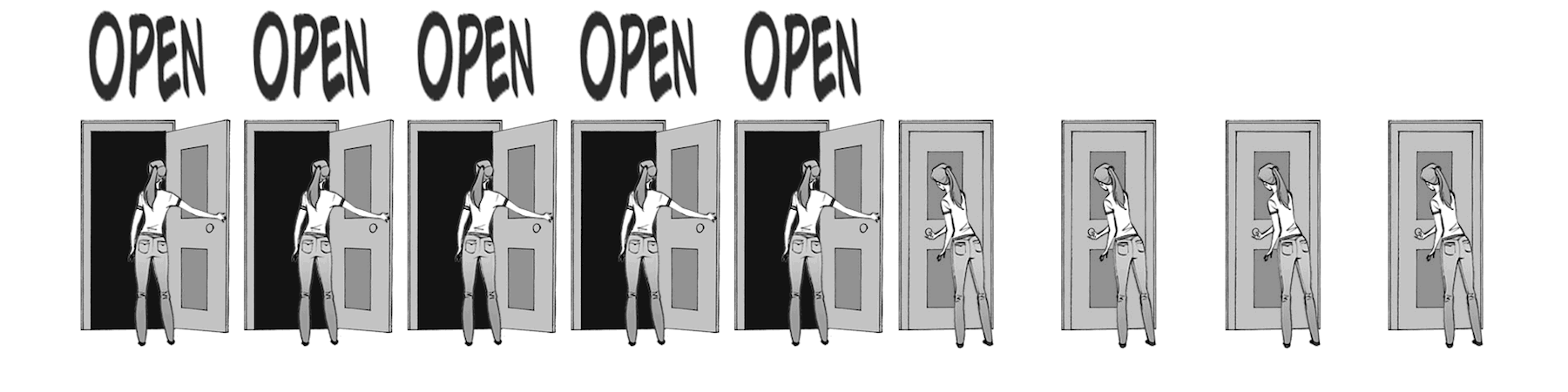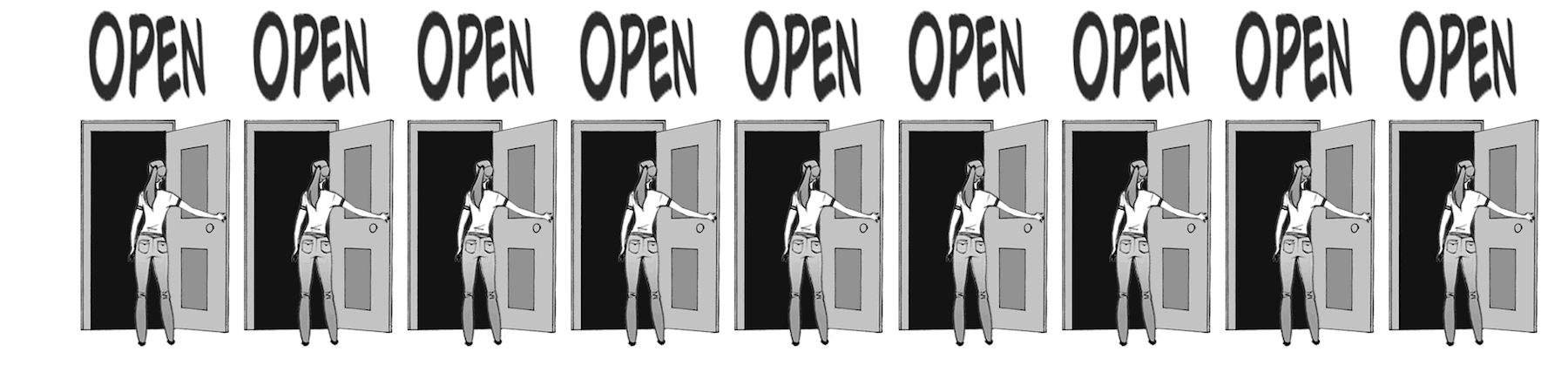
Fig. 3 Imagine a line of doors (ion channels) with people (gates) ready to open them when they hear the full phrase “open.” And, when the vigilant finishes opening their own door, they then repeat the command “Open” which the next person hears. gif from ByB3¶
A space constant can be thought of as a measure of how loud the voice of the vigilants decreeing “open” is. If the “Open” is very loud, many vigilants can hear the open command at once, thus allowing many doors to open at the same time. This is equivalent to a high space constant.
Additional Resources¶
time and space constant text modified from Wyttenbach et al and Backyard Brains.
- 1
Importantly, it does not take any time for the voltage to “travel”. Electrical fields are (practically) instantaneous.
- 2
Covering the neurons with myelin makes the inside and outside of the neural membrane farther apart from each other. As capacitance is affected by the distance of separation between the charged bodies, myelin will decrease cm.
- 3(1,2,3)
Background info for the Experiment: Comparing Speeds of Two Nerve Fiber Sizes